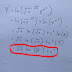2. A rectangle has a parameter of 80 cm. If its width is x, express its length and area in terms of x and find the maximum area
Solution:
FENCE PROBLEM
- A rectangular field is to be fenced off along the bank of a river. If 200 yards of fencing are available, what are the dimensions of a field that produces the maximum area?
TICKET PROBLEM
- Airplane tickets cost $200 if between 0 and 50 passengers are on the plane. However, for each additional passenger over 50, the price per ticket is reduced by $2 for all passengers. For example, if there are 52 passengers, then the cost per ticket for all passengers is $196. How many passengers will produce the maximum revenue?
NIKKO B. BARRAMEDA
Do you live near a river bank? No? Do you like building fences? No? Well, you came to the right blog. I'm here today to show you how to solve an optimization problem about building a fence.
A rectangular field is to be fenced off along the bank of a river. If 200 yards of fencing are available, what are the dimensions of a field that produces the maximum area?
We are finding the area and the measurements of the fence, there we are going to use the equation:
A= xy
STEP 1: FIND Y
STEP 2 : SUBSTITUTE Y TO THE FIRST EQUATION
STEP 3: FIND X
STEP 4: SUBSTITUTE X AND Y TO THE FIRST EQUATION
Now that concludes my Optimization problems about building a fence.
Posted by: Jefferson Duque
A geometry student wants to draw a rectangular inscribed in a semicircle of radius 8. If one side must be on the semicircle's diameter,what is the area of the largest rectangle that the student can draw?
Derrick S. Felizardo
Find the derivative of y=x sin x cos x...
the answer is =sin x cos x + xcos^2-xsin^2x
Derrick S. Felizardo
Does your face look like this during Math class?
If so, then this post is for you! Ease your Math worries (a little bit) by following our step-by-step procedure in solving trigonometric derivatives.
Have you ever seen this equation in your whole life? If you are now shaking your head, then stick around to see the solution!
Step 1
 | ||||||||
| Separate the numerical coefficient |
 |
| Apply the quotient rule |
 |
| Find the derivatives in the numerator |
 | ||
| Simplify the identities |
And there you have it! Solving derivatives should now be almost as easy as pie!
Posted by: Lorraine Suarez
1.
There are two towns on the same side of the river, and the townspeople wants to have a stable supply of water.
Bob is a builder contracted to build a pumping station for their needs. It is to be located at the river’s edge with pipes extending straight to the two towns. The distances are show in the figure below:
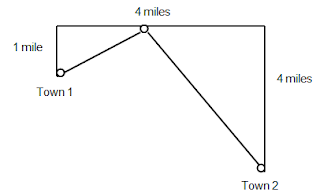 |
| Where should the pumping station be located in order to minimize the total length of pipe? |
Solution:
From the solution above, there are two answers present. It cannot be -4/3, therefore it is 4/5.
Answer:
Posted by: Lorraine Suarez
Car B is 30 miles directly east of Car A and begins moving west at 90 mph. At the same moment car A begins moving north at 60 mph. What will be the minimum distance between the cars and at what time t does the minimum distance occur ?
Assume that the two cars travel at the following rates :
CAR A : 60 mph
CAR B : 90 mph
(distance traveled) = (rate of travel) (time elapsed).
(Equation 1 )
x = 60 t ,
and for car B the distance traveled after t hours is(Equation 2 )
y = 90 t .
Use Equations 1 and 2 to rewrite the equation for L as a function of t only. Thus, we wish to MINIMIZE the DISTANCE between the two cars.
30 - y
Thus the shortest possible distance between the cars is,
L = 24.96 mi.
-Ma. Katrina V. Venta
Differentiate 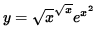
Apply the natural logarithm to both sides of this equation and use the algebraic properties of logarithms, getting,
Thus the final answer is, 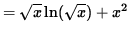 .
.
-Ma. Katrina V. Venta
Copyright 2017. All Rights Reserved. Powered by Blogger.