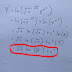Airplane ticket cost $200 if between 0 and 50 passengers are on the plane.
However, for each additional passenger over 50, the price per ticket is reduced by $2 for all passengers.
For example, if there are 52 passengers, then the cost per ticket for all passengers is $196.
How many passengers will produce the maximum revenue?
Optimization Problem
Find the dimension of a small rectangle with an area of 1000 m², whose perimeter
is as small as possible.
Find the derivative of f(x) = tan² (sinx³)
Problem:
A container in the shape of a right circular cylinder with no top has a surface area of 3Ï€ ft.². What height (h) and base radius (r) will maximize the volume of the cylinder?
Answer:
V= Ï€ft.³ is the largest possible volume of the cylinder
2.) Airplane tickets cost $200 if between 0 and 50 passengers are on the plane. However, for each additional passenger over 50, the price per ticket is reduced by $2 for all passengers. For example, if there are 52 passengers, then the cost per ticket for all passengers is $196, How many passengers will produce the maximum revenue?
1.) You are building a cylindrical barrel in which to put Dr. Brent so you can float him over Niagara Falls. I can fit in a barrel with a volume equal 1 cubic meter. The material for the lateral surface costs $18 per square meter. The material for the circular ends costs $19 per square meter. What are the exact radius and height of the barrel so that cost is minimized?
Differentiate:
f(x) = log e (x²+3x+1)
⸫ solutions
Answer:
f(x) = 2x+3
x²+3x+1
We have a piece of cardboard that is 50 cm by 20 cm and we are going to cut out the corners and fold up the sides to form a box. Determine the height of the box that will give a maximum volume.
Solution:
The height of the box will have to be h = 4.4018 in order to get a maximum volume.
A rancher wants to construct two identical rectangular corals using 200ft of fencing. The rancher decides to build them adjacent to each other, so they are fencing on one side. What dimension should the rancher use to construct each coral so that together, they will enclose the largest possible area?
A rancher wants to construct two identical rectangular corals using 400ft of fencing. He decided to build them adjacent to each other so they share fencing on one side. What dimensions should the rancher use to construct each coral so that they will enclose the largest possible area together?
Find the dimensions of the rectangle of largest area that has its base on the x-axis and its other two verticles above the x-axis and lyring on the parabola 2 y = 9-x-3-2-1 0 1 2 3 y = 9x^2
A landscape architect wishes to enclose his rectangular garden on one side by a brick wall costing $30/ft. and on the other three sides by a metal fence costing $20/ft.
If the area of the garden is 1000 square feet, Find the dimensions of the garden that minimize the cost.Let's solve this together!
Now, Let's solve for x!
AND THE ANSWER IS........
44.73 ft
by: Aira Mitra
Problem: Sin3x
__________
4+5 cos2x
Differentiate the function e-3sin4x
Final answer: =e-3x(4cos4-3sin4x)
A closed rectangular container with a square base is to have a volume of 300 in 3. The material for the top and bottom of the container will cost $2 per in 2 and the material for the sides will cost $6 per in 2 find the dimensions of the container of least cost
Let x and y be two positive numbrrs such that x+2y=50 and (x+1)(y+2) is a maximum
In order to reach our destination, we follow traffic rules and drive carefully. The same thing in getting the derivatives of a function, we follow the derivative rules and solve carefully so we can reach for the final and correct answer.
See the picture for an example.
Dyan is in rush with her school works and needs your help. Can you help her by solving this derivative?
FIND THE DERIVATIVE OF
SOLUTION:
ANSWER:
by: Aira Mitra
Every problem has a solution, math problems are no exception.
Just like this optimization problem, it has a solution to be solved.
Problem:
A rectangular sheet of paper with perimeter 36 cm is to be rolled into a cylinder. What are the dimensions of the sheet that give the greatest volume?
Solution: (see the picture below)
Everything has a solution we just have to work hard to come up with the best and right answers.
A container in the shape of a right circular cylinder with no top has surface area 3
ft.2 What height h and base radius r will maximize the volume of the cylinder ?
Final answer: 
ft.3
A ball is thrown straight up in the air from the ground
level. It’s height of after t seconds is given by S(t)= -16t2 + 50t.
When does the ball reach its maximum height?
By: Arvi Velasquez
An engineer is building a rectangular structure with fixed perimeter of 50ft. What dimensions of the largest structure that can be built? What is the area?
By: Arvi Velasquez
By: Daniel Joshua D. Domanais
A baseball team plays in a stadium that hold 55, 000 spectators. With ticket prices at $10, the average attendance had been 27, 000. A market survey showed that for each $0.10 decrease in the ticket prices, on the average, the attendance will increase by 300. How should ticket prices be set to maximize revenue?
By: Daniel Joshua D. Domanais
A open topped-box is constructed as follows: A 24 in x 24 in square botton has four identical squares cut off at each corner. The sides are then folded up.What sized corners should be cut out to maximize the volume of the box. Give this maximum possible
Solution:
By: Ann Caryl Espedido
A rectangle has area is 150 sq in. Determine the dimensions that minimize the perimeter , and give the minimum possible perimeter
Solution:
By: Ann Caryl Espedido
A container in the shape of a right circular cylinder with no top has surface area 3Ï€ ft.2 What height h and base radius r will maximize the volume of the cylinder ?
Caitlin Faye L. Taluban
Build a rectangular pen with three parallel partitions using 500 feet of fencing. What dimensions will maximize the
total area of the pen ?
total area of the pen ?
Engineers are designing a box-shaped aquarium with a square bottom and an open top. The aquarium must hold 500 ft³ of water. What dimensions should they use to create an acceptable aquarium with the least amount of glass?
posted by rei gajo
Let x and y be 2 positive numbers such that x+2y= 50 and (x+1)(y+2) is a maximum.
Solution:
A rancher wants to construct two identical rectangular corrals using 400 ft of fencing. The rancher decides to build them adjacent to each other, so they share fencing on one side. What dimensions should the rancher use to construct each corral so that together, they will enclose the largest possible area?
 |
| rei gajo |
Solution:
